学过物理和化学的人都知道理想气体定律：

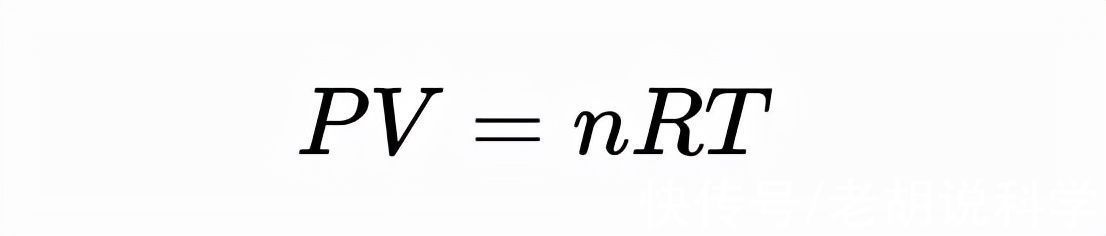
中心课程往往将理想气体定律作为波义耳定律、查尔斯定律、盖-吕萨克定律和阿伏伽德罗定律的组合来教授。这些定律通过经验得到，在本文中我们将采取不同的方法。我将从统计力学、一些定律和一些定义中推导出理想气体定律。

一些定律

对于这个推导，我将只使用理想气体的定义，即热力学定律：

• 第一定律。在一个封闭的系统中，内能的变化等于输入系统的热量减去系统对环境所做的功。

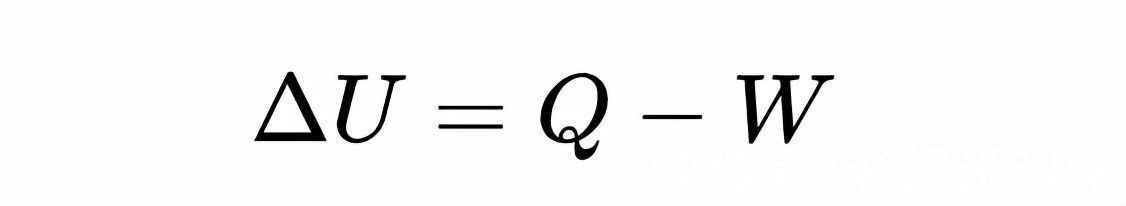
• 第二定律。一个孤立的系统将趋向于它最可能的宏观状态。

(我不需要第三定律，也不会直接使用第0定律，所以这里没有列出来。)

熵的两个定义：

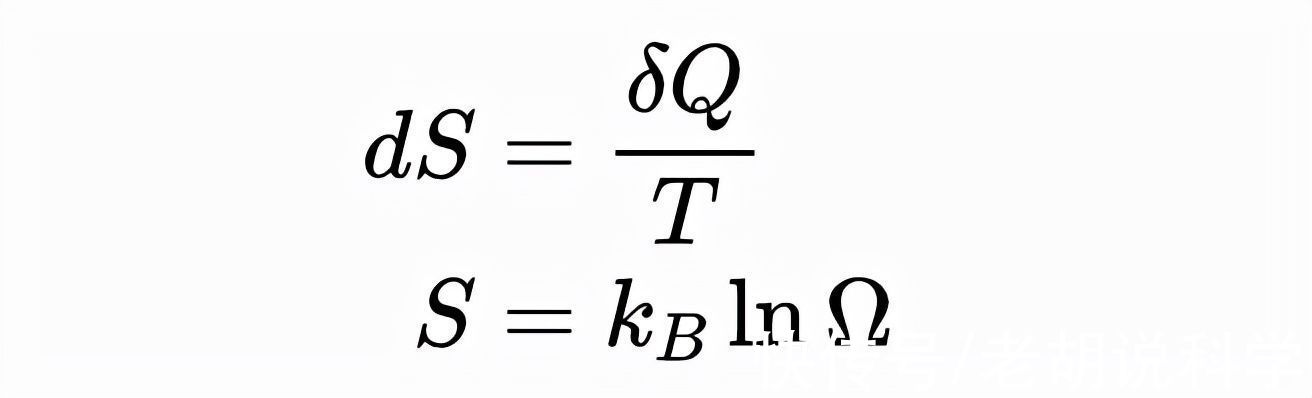
基本计数定理（我将在后面解释），斯特林近似法：

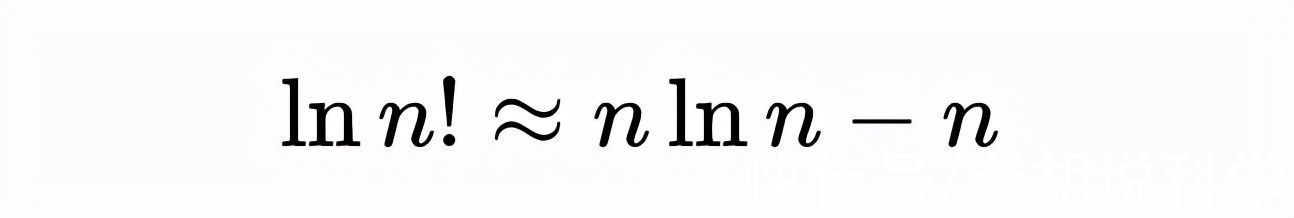
伽马函数：

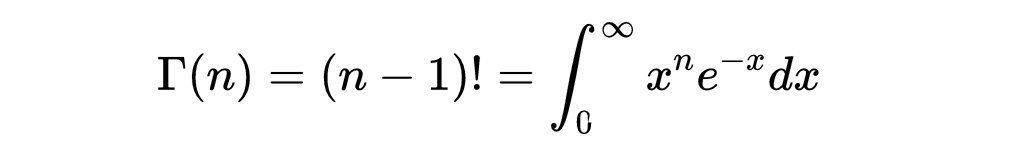
功、压力、温度、体积和粒子数的定义，以及（某种程度上）海森堡不确定性原理：

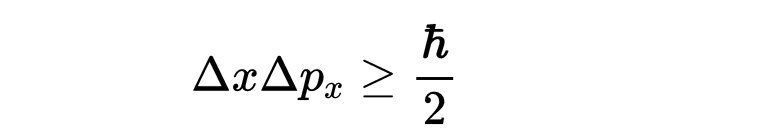
后面我会详细说明为什么需要海森堡不确定性原理。

什么是理想气体？

理想气体是一种由均匀的粒子组成的气体，其中的粒子不相互作用，不占用空间。虽然现实中没有气体具有这些特性，但许多气体由很少相互作用的粒子组成，所占空间可以忽略不计。

理想气体的多重性

因为我们想用统计力学来计算熵，所以我们需要计算理想气体的多重性。

我们将先看一个粒子，以便对我们必须考虑的多重性有一个立足点。然后，我们将转到一个多粒子系统。多重性表示在某些约束条件下可以更改系统的方式的数量。在理想气体的情况下，我们看的是，在给定压强，温度，粒子数量和体积的情况下，选择粒子位置和动量的方法的数量。

我们将首先考虑一个粒子的情况，以在我们必须考虑的多重性中找到一个立足点。然后，我们将研究一个多粒子系统。

一个粒子

让我们考虑一些热力学变量，以及我们如何利用它们来帮助我们推导。

• 粒子的数量。当我们确定使用一个粒子时，粒子数为1。
• 体积。由于我们的模型中的粒子只能在给定的体积内移动，体积限制了可能位置的总数。
• 温度。温度是对气体的平均动能的测量。由于通过熵或能量均分定理转换为内能是很容易的，所以我们不需要它。
• 内能。所有粒子的动能之和必须等于内能。我们可以用动能来寻找动量，所以内能限制了可能的动量的总数。

寻找可能的位置数

我们无法得到所有可能位置的确切数目，因为空间是连续的（暂时这么认为）。可以说，如果有两倍的体积，就有两倍的位置数量，所以我们可以说：

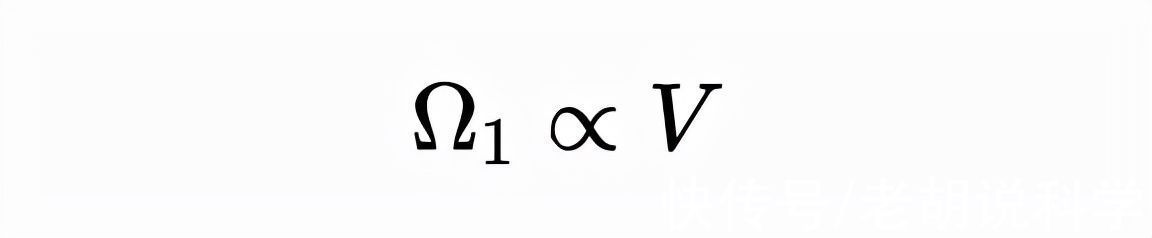
• 一个粒子的多重性与体积成正比。

寻找可能的动量的数量

和位置一样，我们将无法得到所有可能动量的确切数目。推导的过程会有点奇怪。正如我们之前所说的，每个粒子的所有动能之和必须等于内能，这就有了：

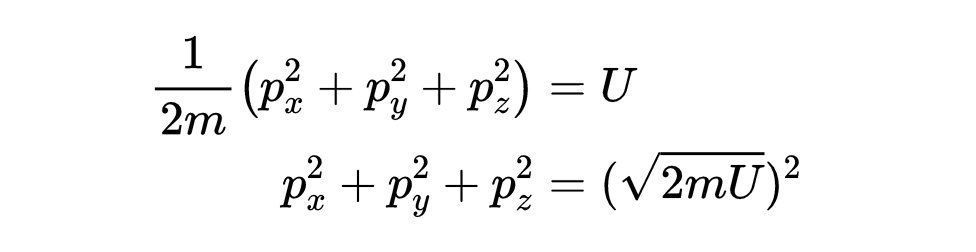
尽管这看起来很奇怪，因为这个方程描述了一个球体的表面。可能的动量的数量与半径为2mU平方根的球体的表面积成正比。

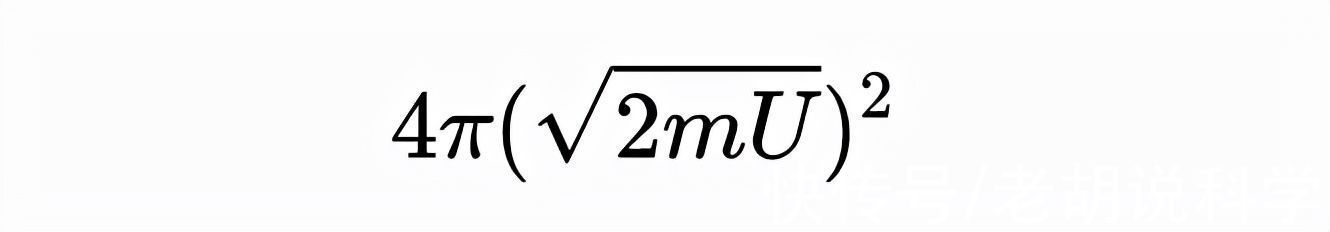
为什么球体会出现在推导过程中？

如果我们看一下动能的方程式，它只包含动量的大小，所以任何具有这个大小的动量都是可能的。给定大小的所有可能向量的集合就是球面的形式定义，所以这就是球出现的原因。

能量等分定理